One Sudoku offers Kendoku puzzles in sizes 3x3 to 6x6. Four difficulties are available for the larger variants. The small sizes 3x3 and 4x4, suitable for beginners, are available in Easy and Advanced. The variants differ in the arithmetic operations (division is required in Expert and Challenging) and the allowed order for subtractions (Easy: only from large to small, for example 6 - 4 - 3, from Challenging onwards other orders can be considered). Starting from the difficulty level Challenging, groups can also contain the same number more than once.


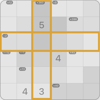
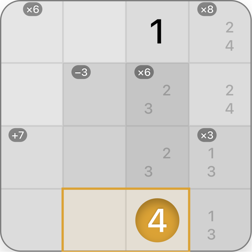
Group
A group is marked in orange. Its result is -1. The arithmetic operation is subtraction. The group consists of 4 cells, one of which is already revealed.


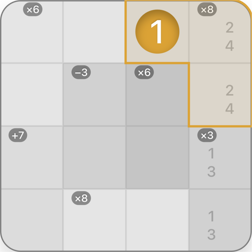
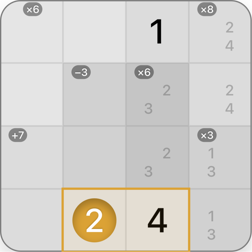
Group
A group is marked in orange. Its result is -1. The arithmetic operation is subtraction. The group consists of 4 cells, one of which is already revealed.