
Cell
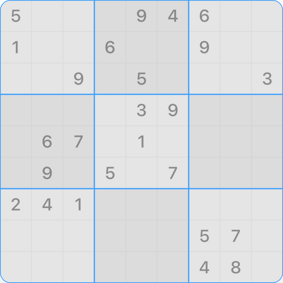
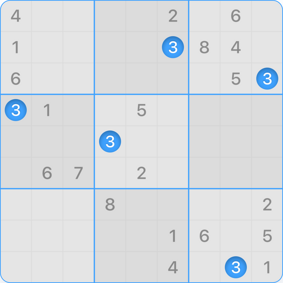
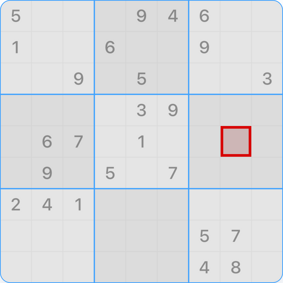
Classic Sudokus in size 9x9 contain 81 cells that can have a value between 1 and 9. Some of these cells are predetermined and therefore visible. Others must be discovered by the player through logical considerations.
Even though numbers have become the most common variant, they can also be replaced by letters, symbols or similar. The only requirement is that they are distinguishable alternatives.


Cell
Classic Sudokus in size 9x9 contain 81 cells that can have a value between 1 and 9. Some of these cells are predetermined and therefore visible. Others must be discovered by the player through logical considerations.
Even though numbers have become the most common variant, they can also be replaced by letters, symbols or similar. The only requirement is that they are distinguishable alternatives.